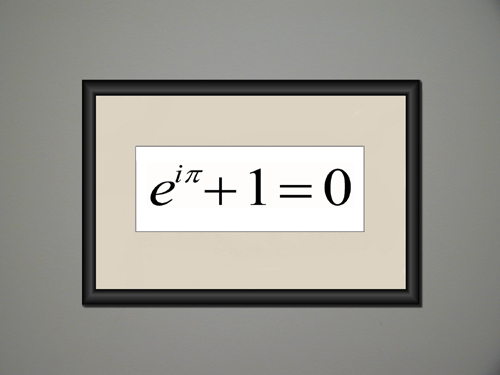
Beauty
100x70cm 1998
Higher resolution
EULER'S RELATION
The British philosopher and logician Bertrand Russell once wrote: "Mathematics, rightly viewed, possesses not only truth, but supreme beauty -- a beauty cold and austere, like that of sculpture."
Russell may well have had Euler's Relation in mind when writing these words.
One of the great wonders of mathematical world, Eulerís relation is like the Grand Canyon, Mount Everest and Niagara Falls rolled into one--what you see depends on how you look at it.
Youíre probably familiar with the famous optical illusion of a painting of an old crone which suddenly changes into a beautiful young woman as your mental perspective changes. Both images are contained within the pictureóthey are different aspects of the same pattern of lines on a page. All you have to do is alter your internal viewpoint to see the difference.
Eulerís relation is a bit like this famous optical illusion but on a vastly grander scale. Imagine walking across a featureless landscape and stumbling across the raw natural beauty of Mount Everest. Youíd have good reason to be pleased with your discovery but as you continue your journey you reach the breathtaking expanse of the Grand Canyon. And beyond that the thundering majesty of Niagara Falls.
The equivalent of Eulerís relation is a final vantage point that shows how all these entirely different wonders of the mathematical world are actually the same. The new perspective simply gives you the insight that connects them together.
Eulerís relation links five of the most fundamental concepts in mathematics in a simple and elegant formula. It says that when viewed in a particular way, the concepts of one and zero are the same as the concepts of the exponential power, e, the imaginary number, i, and the irrational number p.
And yet Eulerís relation is even more powerful. The equation in this work is actually a special case of a broader relation that links two entirely different branches of mathematics--geometry, the study of space, with algebra, the study of structure and quantity. Perhaps that's why the physicist and Nobel Laureate Richard Feynman called it the most remarkable formula in mathematics.
FURTHER READING
Mathworld
and
Planetmath.org offer derivations of Euler's relation
